Sistem Persamaan Linear Tiga Variabel (SPLTV)

Sistem persamaan linear tiga variabel adalah sistem persamaan yang terdiri dari tiga persamaan dimana masing-masing persamaan memiliki tiga variabel. Contoh SPLTV dengan variabel 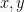$x, y$ dan $z$ :

$\begin{cases} a_1x_1+b_1y_1+c_1z_1=d_1 \\ a_2x_2+b_2y_2+c_2z_2=d_2 \\ a_3x_3+b_3y_3+c_3z_3=d_3 \end{cases}$

dimana $a, b, c$ dan $d$ adalah bilangan-bilangan real.

Pada SPLTV terdapat 2 cara penyelesaian, yaitu:

Metode Subtitusi

Langkah yang dilakukan pada metode ini yaitu:

Ubah salah satu persamaan yang ada pada sistem dan nyatakan $x$ sebagai fungsi dari $y$ dan $z$ , atau $y$ sebagai fungsi dari $x$ dan $z$ , atau $z$ sebagai fungsi dari $x$ dan $y$ ..
Subtitusikan fungsi $x$ atau $y$ atau $z$ dari langkah pertama pada dua persamaan yang lain, sehingga diperoleh SPLDV.
Selesaikan SPLDV yang diperoleh dengan metode yang dibahas pada penyelesaian SPLDV di atas.

Contoh Soal:
Tentukan penyelesaian dari sistem persamaan linear tiga variabel berikut:

$\begin{cases} x-2y+z=6 \cdots (I) \\ 3x+y-2z=4 \cdots (II) \\ 7x-6y-z=10 \cdots (III) \end{cases}$ .

Jawab:

Langkah pertama, nyatakan persamaan (I) menjadi fungsi dari $x$ , yaitu: $x-2y+z=6 \Rightarrow x=6+2y-z$ . Kemudian subtitusikan pada persamaan (II) dan (III), menjadi

Persamaan (II): $3(6+2y-z)+y-2z=4$

Selesaikan, didapat: $7y-5z=-14 \cdots (IV)$

Persamaan (III): $7(6+2y-z)-6y-z=10$

Selesaikan, didapat: $8y-8z=-32$ atau $y-z=-4 \cdots (V)$

Persamaan (IV) dan (V) membentuk SPLDV

Dari persamaan (V), $y-z=-4 \Leftrightarrow y=z-4$ , kemudian disubtitusikan pada persamaan (IV), menjadi:

$7(z-4)-5z=-14$

$7z-28-5z=-14$

$2z=14 \newline \newline z=7$

Kemudian subtitusikan $y=7$ pada persamaan $y=z-4$ diperoleh $y=7-4$ atau $y=3$ .

Subtitusikan $z=7$ dan $z=3$ pada persamaan $x=6+2y-z$ , menjadi $x=6+2(3)-7$ , diperoleh $x=5$ .

Sehingga himpunan penyelesaian adalah $\{3, 5, 7 \}$

Metode Eliminasi

Langkah penyelesaian pada metode eliminasi yaitu:

Eliminasi salah satu variabel sehingga diperoleh SPLDV
Selesaikan SPLDV yang diperoleh dengan langkah seperti pada penyelesaian SPLDV yang telah dibahas
Subtitusikan variabel yang telah diperoleh pada persamaan yang ada.

Soal

Carilah himpunan penyelesaian sistem persamaan berikut:

5x - 3y + 2z = 3
8x - 5y + 6z = 7
3x + 4y - 3z = 15

Jawab :

5x - 3y + 2z = 3  .....(1)
8x - 5y + 6z = 7  .....(2)
3x + 4y - 3z = 15 .....(3) 

Langkah 1 : Eliminasi persamaan (1) dan (2)
5x - 3y + 2z = 3 |x3| ⇔ 15x - 9y + 6z = 9
8x - 5y + 6z = 7 |x1| ⇔  8x - 5y + 6z = 7
                         _________________ _
        7x - 4y      = 2 .....(4)
        
Langkah 2 : Eliminasi persamaan (1) dan (3)
5x - 3y + 2z = 3   ⇔ 15x - 9y + 6z = 9
3x + 4y - 3z = 15 |x2| ⇔  6x + 8y - 6z = 30
        _________________ _
        21x - y      = 39 .....(5)
        
Langkah 3 : Eliminasi persamaan (4) dan (5)
7x - 4y = 3   |x3|  ⇔ 21x - 12y = 6
21x - y = 39  |x1|  ⇔ 21x -   y = 39
                       ______________ _
             -11y = -33
                               y = 3 

Langkah 4 : Substitusi y = 3 ke persamaan (4)
⇔ 7x - 4y  = 2 
⇔ 7x - 4(3)= 2
⇔ 7x - 12  = 2        
⇔ 7x = 2 + 12
⇔ 7x = 14
⇔ x = 2

Langkah 5 : Substitusi x =2 dan y = 3 pada persamaan(1)
⇔ 5x   -  3y   + 2z = 3
⇔ 5(2) -  3(3) + 2z = 3
⇔ 10 - 9 + 2z = 3
⇔ 2z = 2
⇔ z = 1

Jadi himpunan penyelesaiannya adalah {(2, 3, 1)}

Contoh Soal Cerita

Pada suatu hari, tiga sahabat yang bernama Ali, Badar, dan Carli berbelanja di sebuah toko buku. Mereka membeli buku tulis, pensil dan penghapus. Hasil belanja mereka di toko buku adalah sebagai berikut :

Ali membeli dua buah buku tulis, sebuah pensil, dan sebuah penghapus seharga Rp 4.700
Badar membeli sebuah buku tulis, dua buah pensil, dan sebuah penghapus seharga Rp 4.300
Carli membeli tiga buah buku tulis, dua buah pensil, dan sebuah penghapus seharga Rp7.100

Berapa harga untuk sebuah buku tulis, sebuah pensil, dan sebuah penghapus ?

Jawab :

Misal :
x = Harga untuk sebuah buku tulis 
b = Harga untuk sebuah pensil
c = Harga untuk sebuah penghapus

Langkah 1: Buat model matematikanya
2x +  y + z = 4.700 .....(1)
 x + 2y + z = 4.300 .....(2)
3x + 2b + z = 7.100 .....(3)

Langkah 2: Eliminasi persamaan(1) dengan (2)
2x +  y + z = 4.700
 x + 2y + z = 4.300
_____________________ _
 x - y       =  400 .....(4)
 
Langkah3: Eliminasi persamaan(2) dengan (3) 
 x + 2y + z = 4.300
3x + 2b + z = 7.100
_____________________ _
        ⇔ -2x = -2.800
        ⇔   x = 1400
  
Langkah 4: Substitusi nilai x ke persamaan(4)
⇔ x - y = 400
⇔ 1400 - y = 400
⇔        y = 1000

Langkah 5: Substitusi nilai x,y ke persamaan(1)
⇔ 2x +  y + z = 4.700
⇔ 2(1.400) +  1.000 + z = 4.700
⇔    2.800 +  1.000 + z = 4.700
⇔             3.800 + z = 4.700
⇔                     z = 900 

Dengan demikian dapat diketahui :
- Harga sebuah buku tulis adalah Rp1.400, 
- Harga sebuah pensil adalah Rp 1.000, 
- Harga ebuah penghapus adalah Rp 900,

Untuk Tugas bisa klik link berikut : ON PROSES SABAR YA

Mengenal Tampilan dan fungsi-fungsi bagian di dalam Scratch

Pendahuluan berikut tampilan awal scratch Oks. pada blog kali ini kita akan bahas tentang tampilan dan fitur-fitur dari Scratch. di dalam sebuah proyek Scratch terdapat sprite yang akan diisi oleh script maupun audio, lalu apa itu Sprite ? Sprite adalah gambar atau objek yang bisa diprogram . Sprite ini akan berisikan blok blok perintah yang dirancang agar tampil interaktif seperti bergerak, memiliki suara dan lain-lain. Gambar Sprite Default adalah “Kucing Orange”. Sprite kucing ini bisa diganti dengan gambar lainnya. sprite default Scratch Development Environment Keterangan 1. Menu Anda bisa membuat projek baru, membuka projek yang sudah anda simpan, menyimpan proyek yang anda buat, mengganti bahasa atau mencari tutorials. 2. Scripts/Deskripsi Blok Pada bagian kiri, anda akan melihat kode (scripts) yaitu sekumpulan blok blok perintah yang akan digunakan untuk memprogram. Setiap blok pada kode (scripts) memiliki fungsi- fungsi yang berbeda, misalnya saja, perintah Motion, Looks, Sou

Baca selengkapnya

ilmu pengetahuan

Cari Blog Ini