Cara Menyelesaikan Masalah Program Linear

Cara menyelesaikan masalah program linear dapat dikatakan sebagai proses untuk menentukan nilai optimum dari suatu pertidaksamaan. Nilai tersebut dapat berupa nilai maksimum atau minimum, tergantung dari soal yang diberikan. Bentuk umum fungsi objektif dari suatu model matematika adalah f(x,y) = ax + by.

Terdapat dua metode yang dapat digunakan untuk menentukan nilai optimum tersebut, yaitu metode uji titik pojok dan garis selidik. Penjabaran secara lebih jelasnya dapat dilihat pada pembahasan di bawah.

Metode Uji Titik Pojok

Sesuai namanya, metode uji titik pojok dilakukan dengan menghitung nilai fungsi tujuan dari titik pojok yang diperoleh. Titik pojok yang dimaksud di sini adalah titik-titik koordinat yang membatasi daerah layak dari suatu sistem pertidaksamaan linear.

Langkah – langkah yang dilakukan untuk menentukan nilai optimum dengan metode uji titik pojok adalah sebagai berikut.

1. Menentukan garis-garis sistem pertidaksamaan yang menjadi fungsi kendala dari persoalan yang diberikan.
2. Menentukan titik-titik pojok yang merupakan koordinat pembatas daerah yang memenuhi fungsi kendala.
3. Menghitung nilai optimum f(x,y) dari titik-titik pojok yang diperoleh.
4. Mendapatkan nilai maksimum atau minimum sesuai permasalahan.
   

Contoh 1: Tentukan model matematika dari soal di bawah.

Sebuah adonan roti basah dibuat dengan 2 kg tepung dan 2 kg gula. Sedangkan sebuah adonan roti kering dibuat menggunakan 1 kg tepung dan 2 kg gula. Ibu memiliki persediaan tepung sebanyak 6 kg dan gula sebanyak 10 kg. Setiap satu adonan kue basah dapat memberikan untung Rp75.000,00 dan setiap adonan kue kering dapat memberikan untung Rp60.000,00.

Berapakah banyak kombinasi adonan roti yang dapat dibuat untuk mendapatkan keuntungan maksimal?

Pembahasan:

Kita akan membuat model matematika dari soal cerita di atas.

Misalkan:

• x = adonan roti basah
• y = adonan roti kering

Secara ringkas, kebutuhan untuk membuat roti basah (x) dan roti kering diberikan seperti tabel di bawah.

Dari tabel di atas dapat diperoleh model matematika dalam sebuah sistem pertidaksamaan matematika sebagai berikut.

• x ≥ 0
• y ≥ 0
• 2x + y ≤ 6
• x + y ≤ 5
  Jika setiap satu adonan kue basah dapat memberikan untung Rp75.000,00 dan setiap adonan kue kering dapat memberikan untung Rp60.000,00.
  Jadi, fungsi tujuannya adalah memaksimalkan f(x, y) = 75.000x + 60.000y.
  

  Menggambar daerah yang memenuhi sistem pertidaksamaan di atas.

  

  Menentukan titik koordinat yang mennjadi titik pojok pembatas daerah layak dari permasalahan sistem pertidaksamaan.

  Titik Koordinat O, A, dan C dapat diperoleh dengan melihat gambar di atas, yaitu O(0,0), A(0, 5), dan C(3, 0). Sedangkan koordinat titik B dapat diperoleh dengan menggunakan metode eliminasi.

  Mencari koordinat titik B.

  

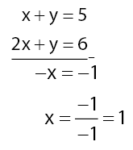
  Substitusi nilai x = 1 pada persamaan x + y = 5 untuk mendapatkan nilai y.

  x + y = 5
  1 + y = 5
  y = 5 – 1 = 4

  Diperoleh koordinat titik B adalah (1, 4)
  

  Perhitungan nilai optimum:

  

  Jadi, nilai keuntungan maksimum yang dapat diperoleh adalah Rp315.000,00 dengan membuat 1 (satu) adonan roti basah dan 4 (empat) adonan roti kering.
  
  2. Seorang pembuat kue mempunyai 8.000 gr tepung dan 2.000 gr gula pasir. Ia ingin membuat dua macam kue yaitu kue dadar dan kue apem. Untuk membuat kue dadar dibutuhkan 10 gram gula pasir dan 20 gram tepung sedangkan untuk membuat sebuah kue apem dibutuhkan 5 gram gula pasir dan 50 gram tepung. Jika kue dadar dijual dengan harga Rp 300,00/buah dan kue apem dijual dengan harga Rp 500,00/buah, tentukanlah pendapatan maksimum yang dapat diperoleh pembuat kue tersebut.

  Pembahasan : 
  
  
  Untuk mengetahui pendapatan maksimum, maka terlebih dahulu kita menyusun sistem pertidaksamaan dan fungsi tujuan dari soal cerita tersebut. Karena yang ditanya pendapatan maksimum, maka tentu harga jual kue merupakan fungsi tujuan pada soal ini. Untuk menyusun sistem pertidaksamaan, yang perlu kita lakukan adalah menentukan variabel dan koefisiennya. 
  
  
  Bahan yang tersedia:
  
  
  Tepung = 8 kg = 8000 g
  Gula = 2 kg = 2000 g
  
  
  Misalkan : 
  
  
  Jumlah kue dadar = x 
  Jumlah kue apem = y 
  
  
  Maka jumlah tepung, gula, dan harga jual merupakan koefisien. Agar lebih mudah, kita dapat memasukkan data yang ada pada soal ke dalam bentuk tabel seperti berikut : 
  
  
  
  
  
  Dari tabel di atas dapat disusun sistem pertidaksamaan sebagai berikut :
  
  
  20x + 50y = 800 ---> 2x + 5y ≤ 800
  10x +5y = 2000 ---> 2x + y ≤ 400
  x ≥ 0 dan y ≥ 0 
  
  
  dengan fungsi tujuan f(x,y) = 300x + 500y 
  
  
  Kemudian gambarkan sistem pertidaksamaan yang sudah disusun dalam grafik. 
  
  
  Untuk garis 2x + 5y = 800 
  x = 0, y = 160 ---> (0, 160) 
  y = 0, x = 400 ---> (400, 0) 
  
  
  Untuk garis 2x + y = 400 
  x = 0, y = 400 ---> (0, 400) 
  y = 0, x = 200 ---> (200, 0) 
  
  
  
  
  
  Sistem pertidaksamaan linear 
  
  
  Titik B merupakan titik potong garis 2x + 5y = 800 dengan garis 2x + y = 400 
  
  
  
  
  
  Selanjutnya substitusikan titik A, B, dan C ke fungsi tujuan : 
  
  
  A(0, 160) ---> F(x,y) = 300(0) + 500(160) = 80.000 
  
  
  B(100, 150) ---> F(x,y) = 300(100) + 500(150) = 105.000 
  
  
  C(200, 0) ---> F(x,y) = 300(200) + 500(0) = 60.000 
  
  
  Jadi, pendapatan maksimum yang bisa diperoleh pedagang kue itu adalah Rp 105.000,00.
  SEMOGA KALIAN MENGERTI SEMOGA BERKAH BELAJARNYA